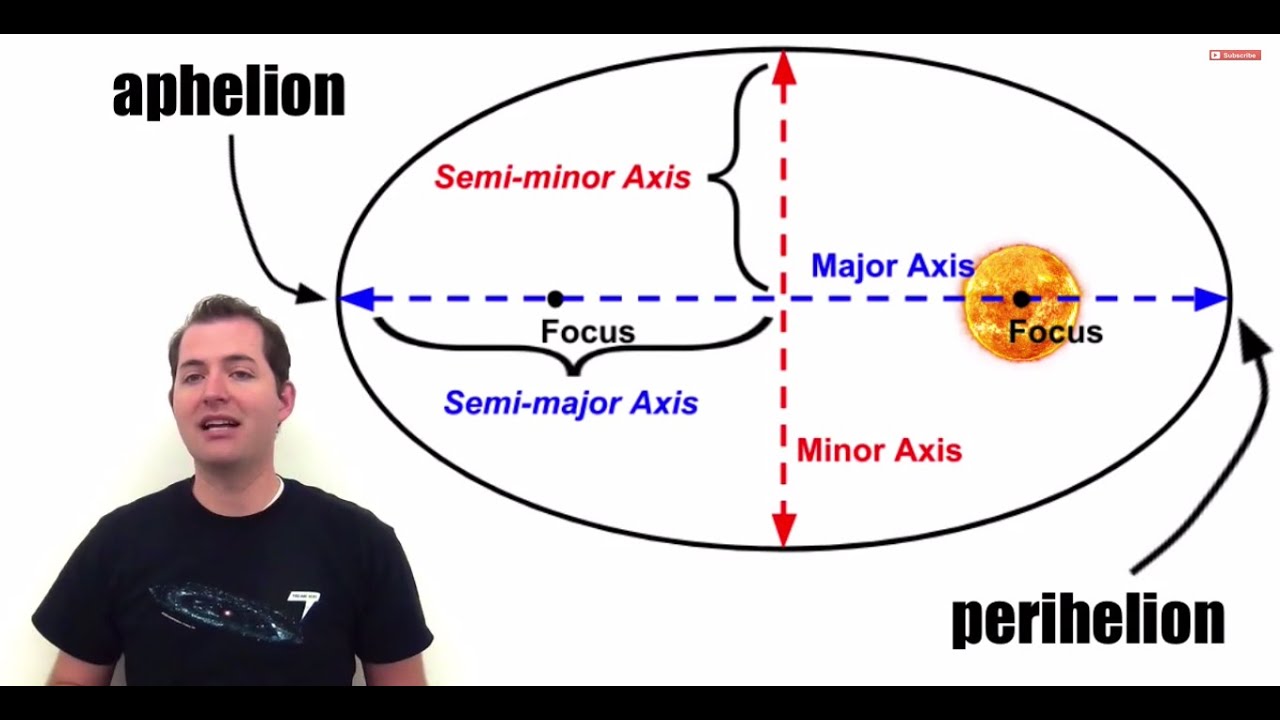
Semi Major Axis and Semi Minor Axis

Im trying find the justification here. The semi-major axis always lies on the line between 0 and PI radians.

Pin On Apologia General Science

More often though we talk about the semi-major axis designated a and the semi-minor axis designated b which are just half the major and minor axes respectively.

. But the limit of the semiminor axis is a finite nonzero length. The semi-major and semi-minor axes of an ellipse are radii of the ellipse lines from the center to the ellipse. With the above relationship being shown it is used to directly show that r s i n v.

The semi-major axis is one half of the major axis and thus runs from the. The semi-minor axis is a line segment that is at 90 degrees with the semi-major axis. ArcGIS Pro 29 API Reference Guide.

It seems simple but I cant figure out why that is. Based on WordNet 30 Farlex clipart collection. The minor is the short axis.

In an ellipse the shorter one. The major axis in an ellipse is the long axis. If the semi-major and semi-minor axes are the same then we have a circle.

Lambda_1 eva1 eva2 lambda_2 evec eigensvectors a rsqrteva1 length of the semi-minor axis b rsqrteva2 length of the semi-major axis arrowsmu1 mu2 b -evec1 2 b -evec2 2 arrowsmu1 mu2 a evec1 1 a evec2 1 axis1 pos mu1 at seq-2 2 1 lty. The semi-major axis is simply the arithmetic mean of the radii at closest and furthest nodes from the systems gravitationally defined center. The longest axis of an ellipse is called the major axis.

Drag any orange dot in the figure above until this is the case. The major axis is the long axis of the ellipse. Another alternative is that we hold one focus and the length of the semimajor axis fixed and move the other focus away from the fixed one.

P avg π 2 a 2 b 2 B 2 ω 2 2R. Semi minor axis of Ellipse is at right angles with the semi-major axis and has one end at the center of the ellipse and is represented as b 2 a or Semi-minor axis 2 Minor axis. 3 π 2 a 2 b 2 B 2 ω 2 2R.

Minor axis is the line segment that is perpendicular to the major axis and intersects at. In a hyperbola the one that does not intersect the hyperbola. Each ellipse has an eccentricity value between 0 a circle and 1 essentially a flat line called a parabola.

The semi-major axis of an ellipse is the longer side and semi-minor axis as the name suggests is the smaller side. The semi-major axis is the larger of the two axes and the semi-minor axis is the smaller axis. ε 0 Bπab ω.

It is one of the axes of symmetry for the curve. This makes defining the semi-minor axis so much easier. I created the ellipse with this expression.

The semi-minor axis also semiminor axis is a line segment associated with most conic sections that is with ellipses and hyperbolas that is at right angles with the semi-major axis and has one end at the center of the conic section. How squashed or off-circle the ellipse. Look at the leftmost point on the ellipse.

And the distance to the further focal point must be. The semi-minor axis also semiminor axis is a line segment associated with most conic sections that is with ellipses and hyperbolas that is at right angles with the semi-major axis and has one end at the center of the conic section. An elliptical loop having resistance R of semi major axis a and semi minor axis b is placed in a magnetic field as shown in the figure.

A Pe Ap 2. Therefore the sum of the distances to the focal points must be. Φ BA cos ωt.

Make_ellipse make_point 00 22 55 72 - thus 22 and 55 for semi-minorsemi-major axis 72 for azimuth. 2 π 2 a 2 b 2 B 2 ω 2 R. In a hyperbola the one that does not intersect the hyperbola.

In geometry the semi-major axis is the distance from the center of an ellipse to the farthest point on the perimeter of the ellipse. In an ellipse the shorter one. 8 rows The semi-major axis major semiaxis is the longest semidiameter or one half of the major.

The term semi clearly rules out the conflict. The minor axis is the short axis of the ellipse. In geometry the major axis of an ellipse is its longest diameter.

As the distance between foci approaches the length of the major axis the eccentricity approaches 1 and the semiminor axis approaches zero. ε dφdt BA ω sin ωt Bπab ω sin ωt. The distance to the closer focal point must be.

Minor axis - the shorter or shortest axis of an ellipse or ellipsoid. Since radii of these two apsis is generally taken as their default values the equation can be simplified. The semi-major axis is half of the major axis which goes all the way across the ellipse at the widest part.

Axis - a straight line through a body or figure that satisfies certain conditions. When we talk about semi-major axis we take half the distance of the major axis. The semi-major and semi-minor axis of an ellipse.

The author says that the ratio b a P R Q R. Relationship Between Semi-Major and Semi-Minor Axes. If they are equal in length then the ellipse is a circle.

Line segment that runs through the center and both foci with ends at the widest points of the perimeter. The semi-major axis is the longest radius and the semi-minor axis the shortest. It is one of the axes of symmetry for the curve.

Half of the major axis is called the semi-major axis. Let a and b be the lengths of the semi-major axis and the semi minor axis respectively of the ellipse with focus S. Make sure you draw a diagram to help you visualize the orientation of the loop with respect to the field and the direction of rotation.

P ε 2 R π 2 a 2 b 2 B 2 ω 2 Rsin 2 ωt Average value of sin 2 θ 12. Semiminor axis - one-half the minor axis of an ellipse. 10 rows The Semi-Major is longest distance longest radius from the central point to the furthest point.

If the loop is rotated about the x-axis with angular frequency ω the average power loss in the loop due to Joule heating is. The shortest axis is called the minor axis. This corresponds almost to half of the values for the widthheight attributes - the ellipse is not really round an contains just the default number of 36 segments hence the.

Eigens eigenA eva eigensvalues note. Jump to navigation Jump to search.

Aerospace Equations Engineering Formulas Equations Orbital Mechanics Engineering

How To Lay Out A Perfect Ellipse Learn Woodworking Woodworking Ellipse

Moon 09 Capital Resources Stock Market Technical Analysis

400 Years Of The Third Law An Overlooked And Neglected Revolution In Astronomy Planetary Astronomy Johannes Kepler

Semi Major Axis Wikipedia The Free Encyclopedia Majors Coding Semi

Oblate Spheroid Surface Area Math Equations Surface

Kepler S Laws Of Planetary Motion Matter Science Teaching Science Earth Science

Rendezvous For Two Students Will Describe The Circular Orbits Of The Space Shuttle And The Internatio Space Shuttle Space Station International Space Station